See our 2022 group poster here!
Frustration and optimal order in filamentous matter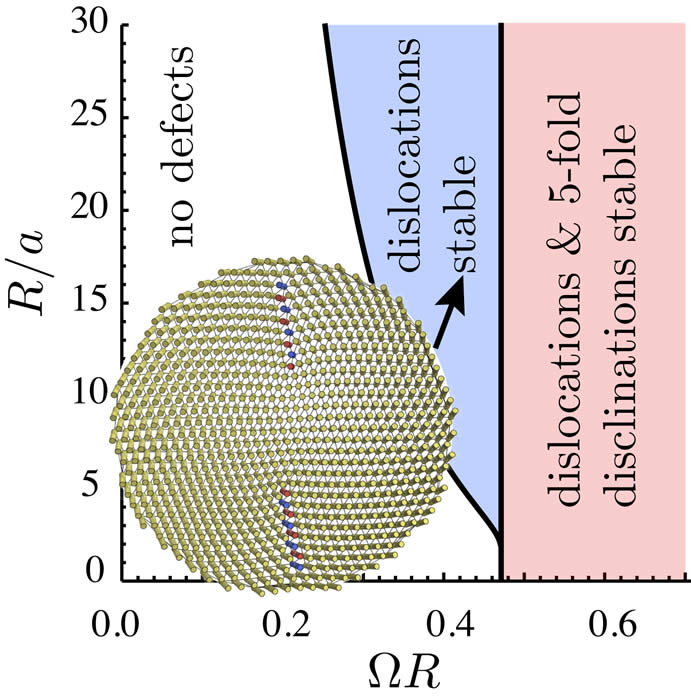
Despite the ubiquity of dense-filament assemblies in such diverse materials as steel cables to textile fibers to nanometer scale assembly of filamentous proteins (cytoskelatal & extracellular fibers) surprisingly little is known about the fundamental rules that govern their assembly and constrain their structure. Our research develops theoretical and computational approaches to the unique geometrical constraints at work in densely-packed filament assemblies and their subsequent impact on thermodynamic, structural and mechanical properties. Biological filament bundles form with an “almost crystalline” degree of cross-sectional order. As models of these materials, our primary efforts focus on the non-linear theory of two-dimensionally ordered filament arrays, so-called, columnar materials. A key result of this analysis is a quan- titative theory of the geometric frustration between the tendency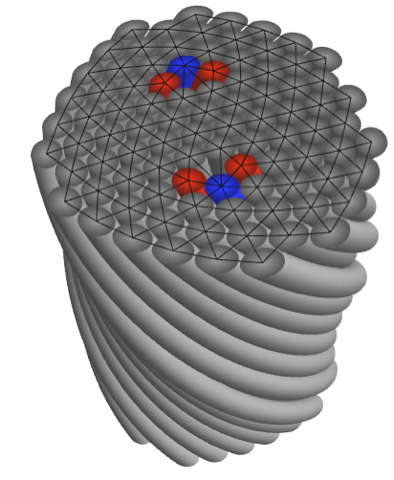
of chiral filaments to mutually twist – a known feature of biological filament interactions – and the preference for isometric, or “constant spacing”, packing of filaments in the cross-section. Simply put, any measure of twist makes it impossible to evenly space filaments in bundles. This geometric frustration begs the question, what is the optimal packing of a twisted bundle or fiber? Much like crystalline order on spherical surfaces, we find that topological defects are necessary components of ground state of twisted bundles. Our recent efforts have focused on understanding the rich and complex spectrum of defect configurations in twisted bundles: in small bundles 5-fold disclinations effectively screen geometric stress while in sufficiently large bundles dislocations and grain boundaries proliferate.
Geometry & thermodynamics of confined chain packing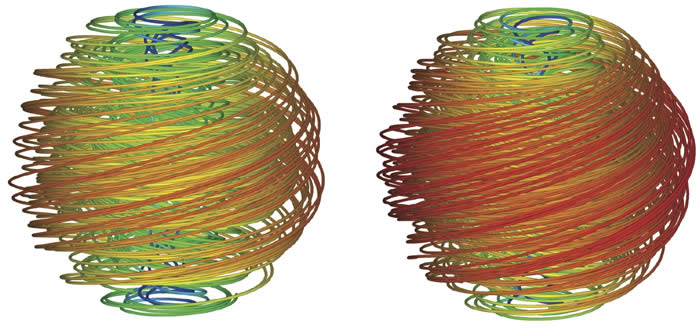
A current thrust our research focuses on the structure and thermodynamics one-dimensional chain packings within a finite, three-dimensional volume. This problem has received considerable attention due to its relevance to bacterial viruses whose dsDNA genome must be enclosed within a roughly spherical capsid of diameter 1000-fold smaller than the chain length. Despite the intense interest in this problem, a number of elementary questions about the structure of confined, densely-packed chains remain unanswered. What is the underlying source of packing frustration? What structures best negotiate the competing geometrical interests of the problem? We have recently developed a "minimal model" of dense, single-chain packing in spherical volumes based solely on three ingredients: i) a vanishing density of chain ends; ii) a preference for parallel orientation of neighbor strands; and iii) a preferred areal density of chains. Within this framework, optimal chain packing becomes a competition between chain ordering at the boundary, which imposes topological defects (point disclinations) at the outer surface, and the elasticity of a divergence-free vector field, describing chain flux in the interior of the packing. Among the packing topologies allowed, only one (with the topology of celebrated Hopf fibration) fills the volume without defects or voids in the interior. Our current goals center on the interplay of the complex polymer nematic order of confined chains and the local 6-fold packing of chains perpendicular to the backbone. Notwithstanding the severe configurational constraints, recent electron microscopy reveals that DNA in virus capsids maintains a surprisingly high-level of local hexagonal order throughout the volume.
Frustrated ordering on complex interfaces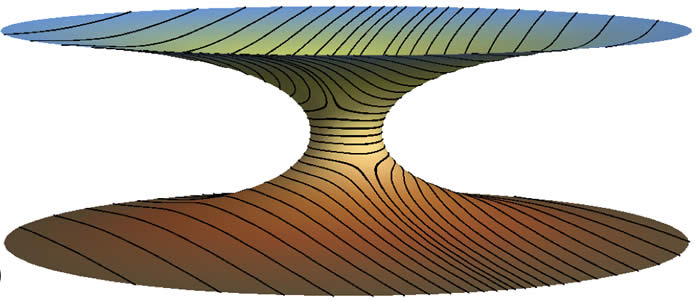
The incompatibility between straight and parallel directions on curved surfaces is a frustration well-known to cartographers and self-organized particles assemblies alike. While rod-like particles easily pack at high densities to adopt well-aligned states on flat surfaces, when these particles assemble at interfaces exhibiting complex geometry -- such as the boundaries in two-fluid mixtures like oil and water -- perfect alignment is impossible. Curvature drives the formation of defects, small regions where the rod alignment breaks down, like the lines of longitude at the poles of the globe. Complicating this already complex state of affairs, we have discovered an additional source of frustration that arises when rods assemble on surfaces which are, themselves, anisotropic, curving like a saddle or a cylinder. This arises because the surfaces themselves have a preferred set of orientations that depends on their geometry. As a result, even when defects are present on anisotropic surfaces they are repelled strongly from highly curved regions of the surface. Depending of the shape and strength curvature alignment, this "extrinsic" frustration may drive a sharp transition in which defects are expel from the surface completely. A quantitative understanding of this mechanism opens up new avenues to tailor the ground states of ordered materials by engineering the underlying surface geometry.
Helical mesophases of chiral block copolymers
Supermolecular, helical assemblies are common structural motifs in far-ranging biological contexts, from the flagellar appendages of swimming microorganisms to the protein coats that sheath rod-like viruses, where screw-like structure of these assemblies ultimately derives from the fact that the subunits from which they are built – proteins and amino acids – are chiral molecules. This strategy may be also employed in synthetic polymer systems, building in helical structure to the assembly from the molecular level up. Block copolymers are well-known to assemble into array of mirror-symmetric, nano-structured patterns, ordered arrays of spherical, cylindrical and layered domains. We have developed a novel theoretical approach to model and predict the self-assembly behavior when one or more constituent blocks is composed of chiral segments. Our theory shows that interactions between chiral segments generically “twist” the trajectories of the self-organized chain molecules. In turn, this twist is transmitted through the tension carried along the chains to the entire assembly, driving otherwise cylindrical assemblies to “buckle” into nanohelices organized in the hexagonal array. These results confirm the notion that mesoscopic, helical 
structure observed lengthscales of 10s of nm in melts of the chiral block copolymer, poly-L-lactide-b-polystyrene, stems from the chiral nature of inter-molecular forces taking place at the nanometer lengthscale, and opens a door to the search for a host of complex meso-chiral structures formed in chiral block copolymer materials, yet to be discovered.